稭稈粉碎機新(xin)聞(wen)動(dong)態(tai)
稭稈粉碎機新(xin)聞(wen)動(dong)態(tai)

富(fu)通(tong)新能源(yuan) > 動態 > 稭(jie)稈粉碎機新(xin)聞動態 > > 詳細(xi)
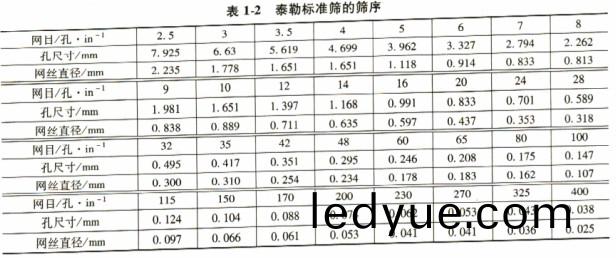
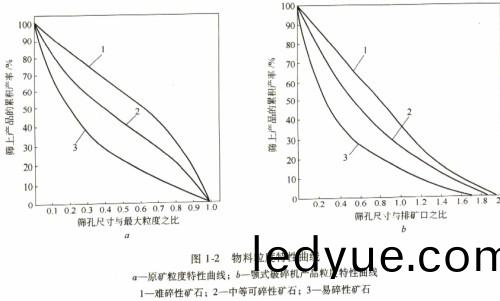
破(po)碎(sui)機(ji)粉(fen)碎(sui)后(hou)的(de)産品(pin)粒形與(yu)粒度(du)分(fen)析(xi)
髮佈(bu)時間(jian):2013-11-04 19:30 來(lai)源:未(wei)知